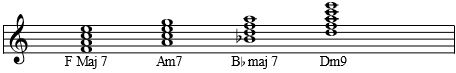Chord Substitution - Overlapping Chords

Now that you have a fair idea of chord construction, you may suspect that some chords may have one or more notes in common with other chords. This is a fact that can be used to good advantage in chord substitution. But obviously, the more notes the substitute has in common with the original chord, the better it's going to be as a substitute.

For instance, the chord Fmaj7 contains the notes F A C E. Am7 has the notes A C E G. B♭maj9 contains B♭ D F A C. And Dm9 contains D F A C E.

Theoretically, it is possible that any one of these four chords could be used as a substitute for one of the others.

Why? Because they all contain so many common notes. All of them contain A and C. Three of them contain A, C and E or F, A and C.

As in all substitution, what works out in theory may not necessarily work out in practice. You must use your own good judgment.

If you keep in mind that substitution does not necessarily mean the complete removal of the original chord, more possibilities will open up to you. For instance, if the original chord is B♭maj9, you might be able to go from that chord to any one or more of the others named above. That means that if the B♭maj9 was only to last for one bar, you may have some quick changing to do.

The easiest way to find alternative chords using this common note method of substitution, is to take the root note of the original chord, go up or down a third, then use that note as a new root to build a new chord.

For instance, using Gm7 (G B♭ D F) as our original chord, we could go up a third and use B♭ as the root of our new chord, possibly trying B♭maj7 (B♭ D F A). We could even try going up another third to D and end up with Dm7 (D F A C).

If we go down a third from the original Gm7 chord, our new root note is E♭ and we might try either E♭maj7 (E♭ G B♭ D) or even experiment with E♭7 (E♭ G B♭ D♭). Going down another third, we would use C as the chord root and could consequently try Cm7 (C E♭ G B♭) as a substitute chord for Gm7.

Following is a table showing the G (natural) minor scale so we can easily work out substitute chords for Gm7 using the common note method. As we will need to go up and down in thirds from the root G, the scale does not begin on the tonic but on the 4th degree; the tonic note, G, is in bold print.

Notice the overlap in adjacent chords in the following music:

Following is a table showing the G major scale so we can work out alternative chords for Gmaj7 using the same method. Again, we begin our scale, not on the tonic, but on the 4th degree; the tonic note, G, shown in bold print.

Note the difference in chord alternatives between G major and G minor. An easier way to remember what alternative chords may be used is that they may be built on the 3rd, 4th, 5th, and 6th degrees of the scale. Both the above tables demonstrate how readily chords can be substituted for their relatives (e.g. Am for C and vice versa).

Understanding Scales | Understanding Chord Structure | Understanding Diatonic Chords | Understanding Minor Scales | Diatonic Chords in Minor Keys | Scale Degree Names | Chord Substitution - Extended Chords | Chord Substitution - Overlapping Chords | Improvisation - Arpeggios | Improvisation - Major Scales | Improvisation - Pentatonic Scales | Improvisation - Blues Scales